Kinematics of the Planar Continuum Snake Robot
New Explorations in Science, Technology + Math, Manhattan
Summer Research Program for Science Teachers
August 2009
Time: 45 Minutes
Level: Students who had a year of Physics, have taken, or are taking, Pre-Calculus/Calculus
Objective:
Students should be able to write down the kinematic equations of the Planar Continuum Snake Robot
Do Now:
Calculate the length of an arc that subtends an angle θ at the center of a circle of radius R.
Motivation:
Throat surgery is unusually challenging because of the shape, length, and complexity of the organ. Snake robots have the dexterity to be used in such and in many others minimally invasive surgical procedures.
Materials:
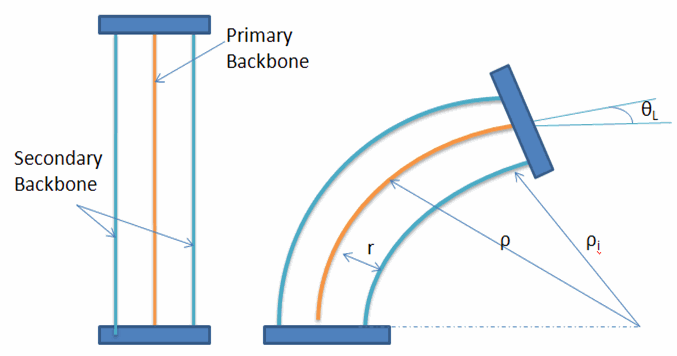
Students will be given snake robots. In addition there will be one drawn on the blackboard as shown below in Figure 1.

Figure 1: Diagram of a snake robot. ρ and ρi are the radius of curvature of the primary and secondary backbones.
Development of Lesson: First identify for the students the primary backbone and the secondary backbone. By pulling/pushing on the secondary backbones, the teacher will bend the robot alternatively in one direction and then in the opposite direction. In groups of two students will work to obtain the kinematics equations of the robot. They goal will be to derive an equation that relates the length of the secondary backbone to that of the primary backbone in terms of θL the angle with respect to the horizontal made by the tangent to the primary backbone.
The teacher will walk around the class speaking to individual groups, encouraging them but not giving them the answer. Ask them to carefully observe the backbones and find out which backbone does not change in length as the robot bends. Once they have answered this question they are well on their way in obtaining the final equation which is,
![]()
Each group must present their work at the end of the class, check for units and explain why they think they are right. In a class of this nature they may be groups that may quickly arrive at the result. Those groups will start programming their equations using MATHLAB.
Summary and Conclusions: I will summarize the main steps in the derivation. I will ask the students to examine again the snake robot and write down the differences they expect between a two dimension and three dimension snake robot that is used in surgery. In this way students will get a better appreciation of the dexterity of a snake robot and their potential in minimal invasive surgery.
STANDARD 1 - Analysis, Inquiry, and Design
Students will use mathematical analysis, scientific inquiry, and engineering design, as appropriate, to pose questions, seeks answers, and develop solutions.
STANDARD 6 - Interconnectedness: Common Themes
Students will understand the relationships and common themes that connect mathematics, science, and technology and apply the themes to these and other areas of learning. Students will understand that models are simplified representations of objects, or systems used in analysis, explanation, interpretation or design.
STANDARD 7 - Interdisciplinary Problem Solving
Students will apply the knowledge and thinking skill of mathematics, science and technology to address real-life problems and make informed decisions.