
Summer Research Program for Secondary School Teachers
William H. Maxwell Career and Technical High School
Brooklyn, NY
August 2004
How do we find the resultant of two vectors at 0°, 90 °, and 180 °?

Two vectors not two members of “The Vectors”!
Objectives: The student will be able to:
1. Use prior knowledge to list several vector quantities
2. Work cooperatively to use their bodies to represent the vectors.
3. Use the head to tail method to draw each resultant, and mathematical methods to solve for each resultant.
Prior Knowledge:
1. Pythagorean Theorem a2 + b2 = c2
2. Experience working in cooperative groups.
3. Definition of a vector and several vector quantities
4. Directions: north, south, east, west, left, right
Do Now: five minutes
Within cooperative groups:
1. List five vector quantities and their units
2. State the reason why these quantities are considered vectors
Motivation:
1. Form Cooperative groups, preferably, of four.
(Teaching Standard E: The activity provides the structure for collaboration between students.)
2. Elicit a response to the Do Now select five groups to give different vector quantities and one to state why these quantities are considered to be vectors.
Answers- Displacement (m), Velocity (m/s), Acceleration (m/s2) Force (N), Weight (N).
A vector quantity is a physical quantity that has both magnitude and direction.
3.Then say the following:
a) All vectors are represented with arrows.
tail ![]() head
head
b) Vectors can be moved anywhere as long as their direction and magnitude are the same.
“shifted to the right”
tail ![]() head
head
c) When finding the resultant of vectors at 0°, 90 °, and 180 ° the head to tail method is used.
3. Say the following: today you will use your bodies to represent different vectors and also to find their resultant. Your arms will represent the vectors, while your head will represent the angle between the two vectors.
(Teaching Standard D – Students are provided with resources, space and time to engage in inquiry-based tasks.)
Lesson:
1. Assign roles: the vector representative, the recorder, the reader, and the reporter.
(Teaching Standard B: Teachers of science guide and facilitate learning. In doing this, teachers challenge students to accept and share responsibility for their own learning.)
2. Within the cooperative groups the students will:
a) Be given a handout “Vector addition at angles 0°, 90°, 180°” and ask them to represent each angle with their bodies as described above. Give the students ten minutes to practice.
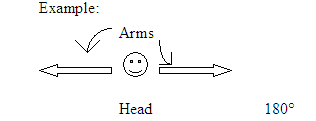
b) Select one group to show the three angles given with their bodies and 0°, 90°, 180° explain each.
c) Have each group now draw each pair of vectors in the handout provided.
3. Say the following: Using the head to tail method, the resultant is drawn from the tail of the first vector to the head of the last vector.
4. Have students draw the resultant for each vector pair (using colored pencil if possible).
5. Ask a student volunteer to reenact the vectors with their bodies, ask two other students to pull on the vectors. Ask the first student to describe the effect on the head, where will it end up? By what magnitude?
Answers
a) 0° - pulled to one particular direction, by a magnitude of both hands pulled.
Ask the following: Well isn’t that similar to adding the vectors?
Have the students write the following below the vector at 0° drawn:
Vectors at 0° (in the same direction) are added to find the resultant.
b) 180° - “my head will split”, it would be pulled in two opposite directions, by a magnitude of both hands pulled.
Ask the following: Well isn’t that similar to subtracting the vectors?
Have the students write the following notes below the vector at 180° drawn:
Vectors at 180° (opposite directions) are subtracted.
c) 90° - The teacher should demonstrate the angle of 90°, and ask a student to show the resultant using a meter stick.
Ask the following: What shape do you see?
Answer: right triangle, elicit the use of the Pythagorean theorem to find the sides of a right triangle. Inform the students that the resultant is the side C.
(Teaching Standard B: Teachers of science guide and facilitate learning. In doing this, teachers challenge students to accept and share responsibility for their own learning.)
Check question:
To see how the method works, consider the following problem:
A hiker leaves a camp and hikes 11 km north, and then 11 km east.
Determine the resultant displacement of the hiker.
a2 + b2 = c2
112 + 112 = c2
c = 15.6 km
Within cooperative groups:
a) Select the vector representative to depict the vector using his/her body.
b) Have everyone draw the vectors.
c) Using the head to tail method draw the resultant
d) Consult today’s handout to solve for the resultant.